以下主要是针对Python3中递归函数介绍和示例。
简单来说,递归就是函数自己调用自己。
但是,自己调用自己不会变成无限循环调用么?
例如下面这个代码:
def recursion():
return recursion()
recursion()代码运行后会抛出异常,RecursionError: maximum recursion depth exceeded
意思是,递归错误:超过最大递归深度
也就是说,因为函数不停的循环调用自身超过了一定次数导致的异常。
这种叫无穷递归(Infinite Recursion),一般来说并没有什么用。
我们需要有用的递归。
比较经典的应用有阶乘运算、幂运算和二分查询(看到这些词语别晕,实际上很简单)。
我们先来看阶乘运算。
阶乘:一个正整数的阶乘是所有小于及等于该数的正整数的积
举例来说,5的阶乘就是5*4*3*2*1,4的阶乘就是4*3*2*1。
其实,阶乘的运算如果不使用递归我们也可以实现。
示例代码:
def factorial(n):
result = n
for i in range(1, n):
result *= i
return result
print(factorial(5)) # 显示输出结果为:120然后,我们来看使用递归方式的实现。
示例代码:
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n - 1) # 函数中调用函数自身
print(factorial(5)) # 显示输出结果为:120递归方式实现的阶乘,好像有些不太容易理解。
我们把计算过程中,参数变量的值通过print语句显示出来看一下。
修改后的代码:
def factorial(n):
print(n) # 显示输出参数值
if n == 1:
return 1
else:
return n * factorial(n - 1)
factorial(5)当我们运行代码,得到如下结果:
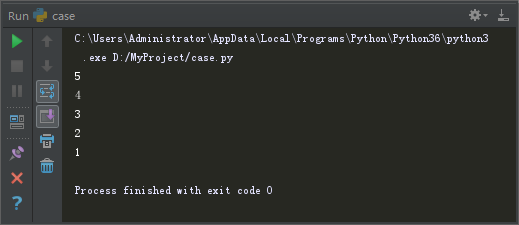
这意味着print语句被执行了5次,同时也意味着函数被调用了5次。
先记下这个特点,我们继续通过print语句把每次通过return语句计算的结果也显示出来。
修改后代码如下:
def factorial(n):
if n == 1:
print('1') # 显示输出当前的阶乘结果
return 1
else:
current = n * factorial(n - 1)
print(current) # 显示输出当前的阶乘结果
return current
factorial(5)当我们运行代码,得到如下结果:
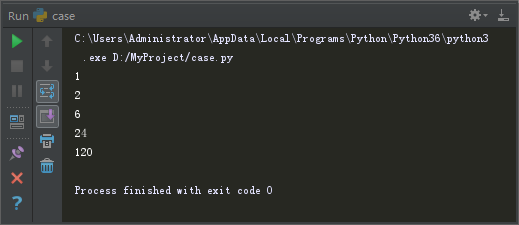
这个结果意味着,每次调用函数都会进行一次计算,并且将计算结果通过return语句返回。
但是,递归的具体执行过程仍然很模糊。
我们来看一个示意图。

上方5个色块,是代码调用了5此函数。
每次调用函数都会创建新的命名空间,大家可以理解为程序执行了5个同名的函数。
既然执行了5个函数,就有参数传入和返回结果的过程。
我们先来看调用函数时,参数传入的过程。
函数首次调用时,参数n的值为5;
首次调用函数的return语句中,进行了第二次调用函数,并设置参数为n-1;所以,在第二次调用的函数中,参数n的值变成了4;
以此类推,直至终止调用函数自身为止。
接下来,我们再来看返回函数执行结果的过程。
程序调用5次函数的同时,进行了参数的传入,第5次调用时,参数n的值是1,;此时,参数数值满足n == 1的条件,不再继续调用函数自身,通过return语句返回值,也就是1;
当1这个值被返回,程序回到了倒数第2次函数调用的return语句,此时语句中对函数的最后一次调用变成了具体的值(1),和变量n相乘之后,作为返回值,再次返回给倒数第3次函数调用的return语句中;
以此类推,直至返回到首次调用的函数为止。
所以,在我们刚才的运行结果截图中,我们能够到,参数的显示结果是5、4、3、2、1的顺序(依次调用函数的顺序);而返回值的显示结果是1、2、6、24、120的顺序(从最后一次调用函数向前返回计算结果的顺序)。
所以,递归可以这么理解,它就是函数循环调用函数自身;递是指在循环调用的过程中,将参数递进下一次函数的调用;归是指当满足终止循环调用函数的条件时,按照和调用时相反的顺序,将函数的执行结果依次回归。
接下来,我们再来看一下幂的计算。
例如,2的4次方实际上是2*2*2*2的乘积。
示例代码:
def power(x, y): # 定义函数计算参数x的y次方
if y == 1: # 满足条件时终止函数循环调用
return x # 参数x的1次方返回参数x
else:
return x * power(x, y - 1) # 调用函数自身形成递归
print(power(2, 4)) # 显示输出结果为:16上方代码中,当我们调用函数power时,函数开始循环调用函数自身,并且依次将参数y(3,2,1)传入每次调用的函数中,当参数y为1的时候,结束函数自身的循环调用,并且依次返回值(2,4,8,16)。
最后,我们再来看一下二分查询的案例。
例如,有一个0~100的数字列表,从中查询到一个指定的数字。
示例代码:
def search(seq, number, lower, upper): # 定义函数,参数seq为要查询的序列,参数number为要查询的数字
# 参数lower为查找区间的下限值,参数upper为查找区间的上限值
if lower == upper: # 查找区间仅剩一个数字时,即找到查询结果,停止循环调用
assert number != seq[upper], '这里有问题!' # 如果不相等会抛出异常AssertionError(断言错误),可以尝试把"=="改为"!="
print(str(lower)) # 显示输出结果为:66
else: # 查找区间有多个数字时,继续查找
middle = (lower + upper) // 2 # 通过整除计算,获取查找区间数字的中间值
if number > seq[middle]: # 判断查找的数字是否大于中间值
return search(seq, number, middle + 1, upper) # 如果大于中间值,中间值作为查找区间下限值,继续查找
else:
return search(seq, number, lower, middle) # 如果小于中间值,中间值作为查找区间上限值,继续查找
search(range(0, 100), 66, 0, 100) # 显示输出结果为:66大家根据代码中的注释对递归过程进行理解,在此不再赘述。
不过在上方代码中,我添加了一个assert关键字,此关键字为断言,可以帮助我们运行程序检查语句中的错误。
使用格式为:assert 表达式, ‘自定义的异常说明字符串’
自定义的异常说明字符串可以省略,未省略时,字符串和表达式之间必须用逗号(,)分隔。
如果断言语句中的表达式出现错误,则会抛出AssertionError异常。
如果自定义了异常说明字符串,则会显示“AssertionError:自定义的异常说明字符串”。
