八皇后问题是一个古老而又著名的问题,是学习回溯算法的一个经典案例。
先来看一个场景:
有若干组门,每组有两个门,一扇门后面可以通行,另一扇门后面堵塞,需要找出正确的路线。
如果想找出正确的路线,只能打开任意一扇门,如果通行则记下当前这扇门,然后继续往前,如果堵塞则退出后从另外一扇门通过,并且记下另外一扇门,以此类推,直到走过所有的门。
大家先看下图的左侧(示例代码结合右侧进行理解),理解找出正确路线的过程。
这里,以4组门并且每次先进入左侧门为例。
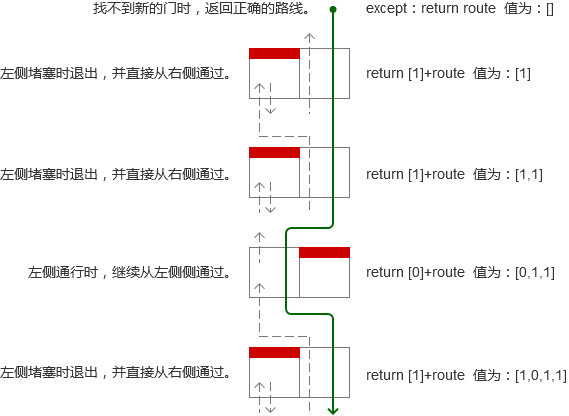
递归就类似这样的场景,每次都用同样的方法去找出正确的门,不同的只是是每次的门不是同一组。
接下来,我们就来看如何通过代码找到路线。
我们把每一组门进行编号,左侧为0,右侧为1。
示例代码:
def go(doors, count=0, route=[]): # 参数doors为多组门的列表,参数count为每组门的序号,参数route为路线列表。
try: # 捕捉列表索引超出时的异常(走过最后一组门之后,找不到新的门。)
if doors[count][0] == '通行': # 打开左侧的门,查看是否通行。
return [0] + go(doors, count + 1)
# 如果通行,将左侧的门编号暂存(和之后所有正确的门编号一起返回),并进入下一组门。
else: # 否则
return [1] + go(doors, count + 1)
# 进入右侧的门,将右侧的门编号暂存(和之后所有正确的门编号一起返回),并进入下一组门。
except: # 异常处理(找不到新的门)
return route # 返回正确路线。
doors = [('堵塞', '通行'), ('通行', '堵塞'), ('堵塞', '通行'), ('堵塞', '通行')]
print(go(doors))这个打开多组门寻找正确路线的案例,比较简单。
接下来,我们来看一个比较经典的题目:八皇后
这个题目是说有八个皇后(种马风格…),皇后与皇后之间不能互搞(禁止女同…)。
也就是每个皇后与其他皇后不能再同一条水平线、垂直线、以及对角线上。
我们需要通过代码,计算出所有的摆放方法,也就是把每一种摆放方法以列表或元组的形式生成。
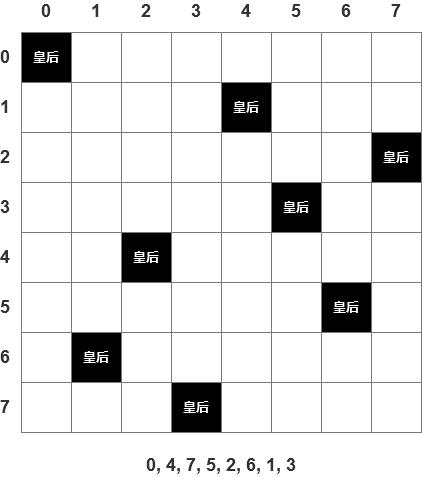
如下图:“0, 4, 7, 5, 2, 6, 1, 3“,就是一种正确的摆放方法。
我们编写代码基本都是为了解决某些问题,而解决问题的先决条件是理清思路,这样才能找出解决问题的方法。
接下来分析一下八皇后的解题思路。
首先,我们模拟一下寻找所有摆放方案的过程。
1、棋盘有8行8列,按由上至下的顺序摆放的话,每一行只能有一个皇后。
2、当我们在第1行任意位置(列)摆下皇后,第2行摆放皇后的时候,就不能与第1行的皇后在同一列或同一对角线上。而第3行摆放的时候,不但要注意不能与第1行的皇后有冲突,也要注意不能与第2行的皇后有冲突。
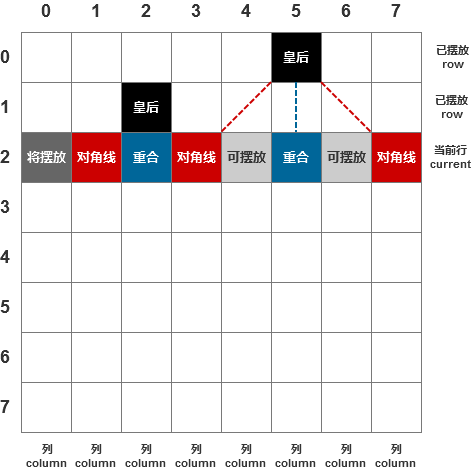
3、每一行的每一列都要尝试摆放,直到找出所有摆放方案。
4、每一行摆放时,如果有可摆放的位置,摆放皇后之后进行下一行的摆放,否则,放弃当前行的摆放。
5、如果摆放的是最后一行,仍然能够找到合理的摆放位置,将结果生成;否则,继续下一行摆放。
接下通过代码,实现上面的过程。
首先,解题的关键在于如何确定当前行皇后的摆放位置与之前所有已摆放皇后的位置不冲突。如果与之前皇后位置重合的话,列编号相同,也就是列的间隔为0;如果与之前皇后位置处于对角线的话,列的间隔与行的间隔相同。这里要注意,摆放位置在左侧对角线时,计算的间隔结果为负数,而右侧对角线计算间隔的结果是正数,所以,计算间隔时还需要计算绝对值。
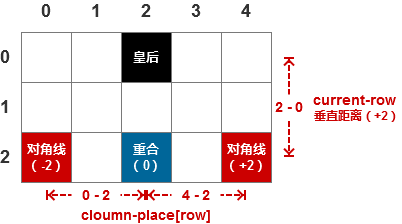
然后,我们可以通过元组或列表保存每一次正确的摆放方案,元组或列表中元素的编号(0-7)为行编号,而元素本身为列编号(每一行摆放的位置)。如果通过列表保存,可以先创建一个长度为8的列表,修改列表中的每一个元素;如果通过元组保存,可以创建一个空元组和每一行正确的摆放位置相连接。
这里,我们通过元组保存结果,来完成这个题目。
示例代码:
def check(place=(), column=0):
# 定义检查位置的函数,参数place为已正确摆放皇后位置的元组,参数column为最新一行将要摆放皇后的位置(列编号)。
current = len(place) # 获取当前摆放行的编号
for row in range(current): # 遍历当前行之前的每一行
if abs(column - place[row]) in (0, current - row):
# 检查当前行摆放皇后的列与任何一行摆放皇后的列,是否重合或者处于对角线。place[row]为每一行皇后所处的位置(列编号)。
return False # 如果检查到皇后的位置有冲突,则返回假值。
return True # 默认返回真值
def queen(place=()):
for column in range(8): # 轮流将皇后摆放到行的每一列
if check(place, column): # 判断当前行皇后的位置是否与其它已摆放皇后的位置处于同一列或者对角线的位置
if len(place) == 7: # 如果是最后一行
yield (column,) # 生成最后一行列的元组
# yield place + (column,) # 生成最终结果(方案2:替代上一句)
else: # 否则
for result in queen(place + (column,)): # 获取递归生成的结果
yield (column,) + result # 生成当前行的列与递归生成的结果组成的新元组
# yield result # 生成递归生成的最终结果(方案2:替代上一句)在上方代码中check()函数负责检查当前皇后摆放位置是否与之前皇后摆放位置有冲突。
另外,在上方代码中,yield语句有两种方案,大家可以替换尝试。
最后,我们还可以将生成的摆放结果,以图形的形式显示输出。
在上方代码的基础上,继续添加代码。
示例代码:
from random import choice # 从随机模块中导入随机选择的方法
gen = queen()
ran = choice(list(gen)) # 随机获取一个生成结果存入变量
print(ran)
for i in ran:
print('□ ' * i + '■ ' + '□ ' * (7 - i)) # 注意特殊符号后方都带有一个空格显示输出结果类似下方内容:
(7, 2, 0, 5, 1, 4, 6, 3)
□ □ □ □ □ □ □ ■
□ □ ■ □ □ □ □ □
■ □ □ □ □ □ □ □
□ □ □ □ □ ■ □ □
□ ■ □ □ □ □ □ □
□ □ □ □ ■ □ □ □
□ □ □ □ □ □ ■ □
□ □ □ ■ □ □ □ □
最后,再为大家呈上通过列表完成的代码。
这段代码中,思路和上方代码一样,不过没有把检查冲突的代码独立抽出为函数。
示例代码:
def queen(place=[None] * 8, current=0):
# 定义皇后摆放方法,参数place为摆放位置列表,参数current为当前要摆放皇后的行(简称:当前行)。
for column in range(8): # 尝试将皇后摆放到行的每一列
place[current], mark = column, True # 在当前行的每一列轮流摆放皇后,并且设置标记为真值。
for row in range(current): # 遍历当前行之前的每一行
if abs(column - place[row]) in (0, current - row):
# 检查当前行摆放皇后的列与任何一行摆放皇后的列,是否重合或者处于对角线。
mark = False # 设置标记为假值,即当前行摆放皇后的位置和其他行摆放皇后的位置有冲突。
break # 跳出对每一行皇后摆放位置的检查
if mark: # 如果检查皇后摆放的位置没有冲突
if current == 7: # 如果当前行是第8行
yield place # 生成最终结果
# yield tuple(place) # 如果使用list()函数获取全部生成结果需要转换为数组,否则都是[7,7,7,7,7,7,7,7]。
else: # 否则
for result in queen(place, current + 1): # 获取递归生成的最终结果
yield result # 生成递归生成的最终结果